2021.01.09
教育ログデータ その3
さらに詳細にデータの読み方を見てみましょう。今回テーマとして取り上げるのは、平均解答時間と正答率で散布図を作成し、それをどの様に読み解くかです。
前回、
「点数(正答・誤答の比)×解答に要した時間」
を見ると良いという話をしました。実は1問1問をチェックしていれば、ある難易度の問題から解答時間が突然長くなるようであれば、そこが学習者が詰まっているポイントだと考えることができます。これによって、その単元でどれくらいの理解度まで到達しているかを把握することができます。しかし、事前テストと事後テストでの理解度を、個別および全体として把握するためには、このやり方は手間です。そこで、今回は点数を「正答率」として扱います。
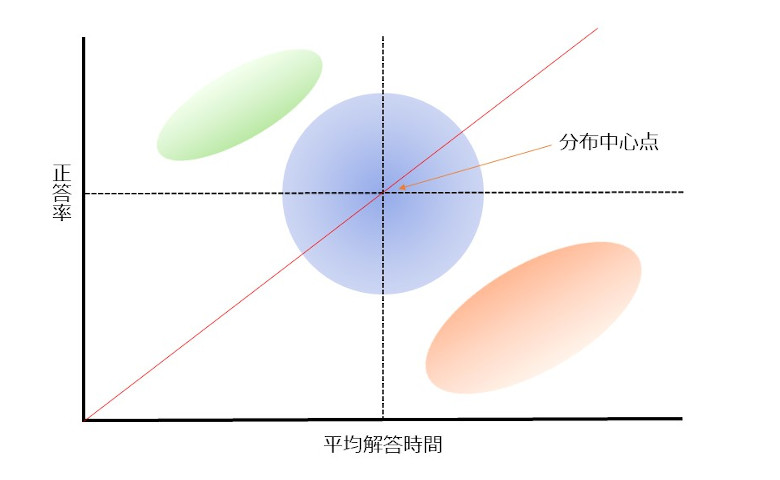
縦軸は学習者それぞれの全問題のうち何問正解したのか、を正答率として設定します。横軸は1問を解くのにかかった平均解答時間とします。これで散布図を作ってみると、集団全体の平均正答率と、同じく集団全体の平均解答時間を中心(以下、分布中心点)に、分布することが想定されます。
そこで、原点と分布中心点を結ぶ線を引いてみます。するとこの線上に乗っている学習者は平均的な能力を持っていると考えることができます。一方、この線より左上(緑色の部分)に分布している学習者は、平均よりも理解できていると考えられ、逆に右下(橙色の部分)に分布する学習者は平均よりも理解度が低いと考えられます。
とはいえ、線より下に分布した学習者がすべて対策すべき人々ではありません。というのは、分布はある程度ばらける(青色の部分)からです。したがって、この分布範囲を考えながら一定の基準を策定し、それよりも下に分布する学習者に対して対策を打つべきです。
一方、分布がばらけることを考えると、一定の基準よりも成績が良い学習者に関しては、このテストは簡単であったとみなすべきでしょう。もっと先に進めるための対応をする必要があります。
さて、ではこの散布図において、事前テストと事後テストの関係性を考えます。学習によって理解が進んだ場合、事後テストの結果は事前テストと比較した場合、どの様に移動するでしょうか。基本的には理解が進んで欲しいわけですから、
①正答率が上がる
②平均解答時間が短くなる
のどちらか、または両方を満たすことが求められます。つまり、事前テストの成績と比較した場合、上に移動するか、左に移動するかです。最も良いのは左上方向に移動することだと言えます。
一方、右上方向への移動は、例え正答率が上がったとしても、理解度が上がったとは見なせません。また右下方向に下がった場合は、理解度が下がったことを意味しますので、もしかなり右下方向に移動してしまった場合は、その学習者に対しては指導の仕方がまずかったと考えることができます。
このように、全体としては「正答率×平均解答時間」の散布図を作成すると、いろんな事が分かるようになります。
Written by T.T.Yamada
学習ログを取ることで、弱点分析や学習態度を分析する
eラーニングシステム。PC、タブレット、スマホに対応